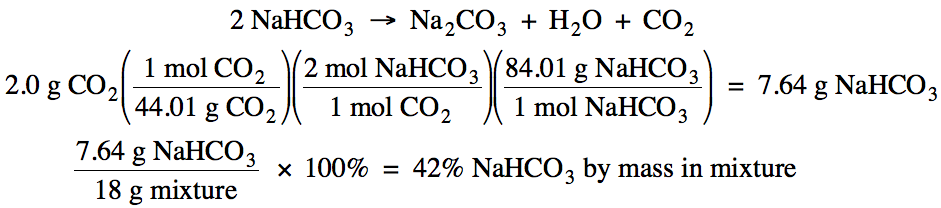Chapter 4: Balancing Chemical Equations and Stoichiometry
Section 4-1: Balancing Chemical Equations and States of Matter
Section 4-2: Mole Ratios and Stoichiometry
Section 4-3: Limiting Reagents
Chapter 4 Practice Exercises and Review Quizzes
Section 4-1: Balancing Chemical Equations and States
of Matter
In a balanced chemical equation,
the number of atoms of a particular element among the reactants on the left
side of the arrow will be equal to the number of atoms of that same element
among the products on the right side of the arrow. To balance a chemical equation, you may only change the
coefficients that are written before each reactant and product. However, you may NOT change the subscripts in any chemical formulas as that
would change the identities of the substances involved in the reaction. The problem below demonstrates key
reasoning that may be utilized when balancing chemical equations:
Sample Exercise 4A:
Balance the following chemical
equations using the smallest possible whole-number coefficients:
(a) P4 + Cl2 → PCl3
(b) C3H7OH +
O2 → CO2
+ H2O
Solution:
(a) Since there are 4 P atoms on
the left but only 1 P atom on the right originally, we start by placing a
coefficient of 4 in front of the PCl3 so that there will be 4 P
atoms on both sides:
P4
+ Cl2 → 4 PCl3
Because there are now 12 Cl atoms on the right (coefficient of 4 x subscript of 3 = 12) but only 2 Cl
atoms on the left, we then place a coefficient of 6 in front of the Cl2
so that there will be 12 Cl atoms on both sides:
Final Balanced Equation: P4 + 6 Cl2 → 4 PCl3
(b) It is wise to begin by
balancing those elements that only appear in one substance on the left and one
substance on the right. Thus, we
will balance the C and H atoms first but wait to balance the O atoms as they
appear in more than one substance on both sides of the equation.
Since there are 3 C atoms on the
left but only 1 C atom on the right originally, we start by placing a
coefficient of 3 in front of the CO2 so that there will be 3 C atoms
on both sides:
C3H7OH
+ O2 → 3 CO2
+ H2O
Since there are 8 H atoms on the
left but only 2 H atoms on the right, we then place a coefficient of 4 in front
of the H2O so that there will be 8 H atoms on both sides:
C3H7OH
+ O2 → 3 CO2
+ 4 H2O
At this point, there are 10 O atoms
on the right. Since there is
already 1 O atom in the C3H7OH on the left, we will need
to change the coefficient in front of the O2 in order to add 9 more
O atoms. We can temporarily balance
the equation by using a fraction in front of the O2:
C3H7OH
+ 9/2 O2 → 3 CO2
+ 4 H2O
Although it is acceptable in
certain situations to use fractions to balance a chemical equation, we were
asked in this case to use the smallest possible whole-numbers, so we then
multiply all coefficients in the equation above by 2 to eliminate the fraction
while keeping the equation balanced with 6 C atoms, 16 H atoms, and 20 O atoms
on both sides:
Final Balanced Equation: 2 C3H7OH + 9 O2
→ 6 CO2 + 8 H2O
Throughout this textbook, we may
also indicate the state of matter of each reactant and product in a chemical
equation as follows:
|
State of Matter |
Abbreviation |
|
Gas |
(g) |
|
Liquid |
(l) |
|
Solid |
(s) |
|
Aqueous
(Dissolved in Water) |
(aq) |
Section 4-2: Mole Ratios and Stoichiometry
Stoichiometry is essentially the study of
the quantities of substances in a chemical reaction. Once a chemical equation has been balanced, we will then
know the ratios of the moles of all reactants and products involved in the
reaction. For example, consider
the second reaction that we balanced in the previous section:
2 C3H7OH + 9 O2
→ 6 CO2 + 8 H2O
Based on this balanced equation,
the reactants react and the products are formed according to the following
ratios:
2 mol C3H7OH:
9 mol O2: 6 mol CO2: 8 mol H2O
Therefore, if we know the moles of
any reactant or product involved in the reaction, we can find the unknown moles
of any other reactant or product using dimensional analysis and the mole ratios
above. For example, if 12 moles of
C3H7OH react, we can find the moles of O2 that
react and the moles of CO2 formed as follows:
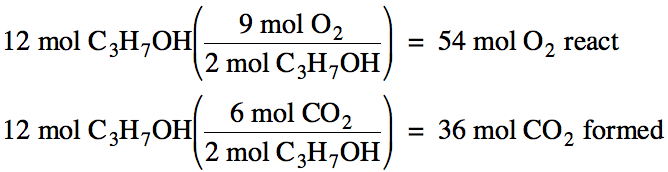
Although the mole ratio will be a
central step in each stoichiometry problem, you may
first need to convert from another unit to moles of the known reactant or
product and then end by converting moles of the unknown reactant or product to
another unit:
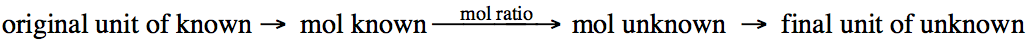
The following problem will
demonstrate a common type of stoichiometry problem
where both the original and final units are grams:
Sample Exercise 4B:
Given the unbalanced equation
below, what mass of C2H5SH must react in order to produce
0.030 grams of water?
C2H5SH + O2
→ CO2 + H2O + SO2
Solution:
First, balance the equation:
2 C2H5SH + 9 O2
→ 4 CO2 + 6 H2O + 2
SO2
Next, convert the known mass of
water to moles, then use a mole ratio to convert to
the unknown moles of C2H5SH, and finally convert to grams
of C2H5SH:
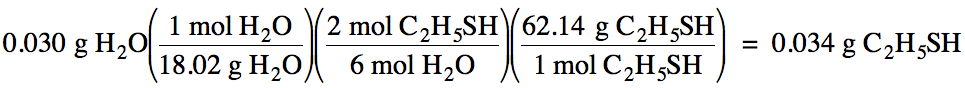
If a known mass of a mixture contains
one reactive component with the remainder being unreactive, stoichiometry can
be used to determine the percent by mass of the reactive component in the
mixture. Starting with the mass of
one product, we can use stoichiometry to determine the mass of the reactive
component in the mixture, which then allows us to determine the percent by mass
of that reactive component in the mixture. This process is demonstrated below in Practice Exercise 4-5.
Section 4-3: Limiting Reagents
When two reactants are mixed to
initiate a chemical reaction, one of the reactants may be used up completely
while some of the other reactant may remain after the reaction is
complete. The reactant that is
used up completely is called the limiting
reagent (or limiting reactant).
We can use the initial amount of the limiting reagent and stoichiometry to determine the maximum amount of any product that
can form in the reaction. The
reactant that still remains after the reaction is complete is known as the excess reagent (or excess reactant), and
we can calculate the amount of the excess reagent that remains using stoichiometry and subtraction. The following problem demonstrates how to identify the
limiting reagent as well as how to calculate the maximum amount of product that can
form and the amount of the excess reagent that remains:
Sample Exercise 4C:
Given the unbalanced equation
below, if 31.6 grams of CS2 is mixed with 17.0 grams of NaOH:
(a) Which is the limiting reagent?
(b) What maximum mass of Na2CS3
can form?
(c) What mass of the excess reagent
remains when the reaction is complete?
CS2 + NaOH
→ Na2CS3 + Na2CO3
+ H2O
Solution:
First, balance the equation:
3 CS2 + 6 NaOH → 2 Na2CS3
+ Na2CO3 + 3 H2O
Next, read through the entire
problem to determine which product is being investigated. In this case, we are trying to find the
mass of Na2CS3.
As such, use stoichiometry to calculate which
reactant can produce a lower mass of Na2CS3. The reactant that can produce less Na2CS3
is the limiting reagent, and the mass of Na2CS3
calculated from the limiting reagent will be your answer to (b).
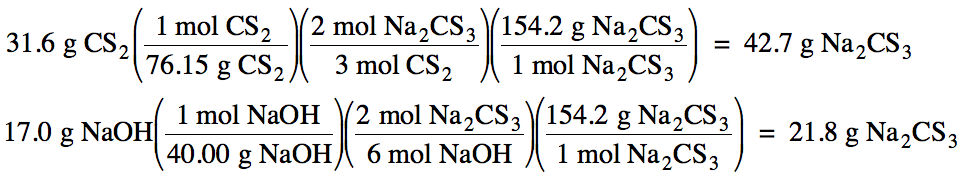
(a) NaOH
produces less Na2CS3, so NaOH
is the limiting reagent.
(b) 21.8 g Na2CS3
maximum can form.
(c) Use the mass of Na2CS3
that can form from the limiting reagent and stoichiometry
to calculate the mass of the excess reagent, CS2, used up in the
reaction:
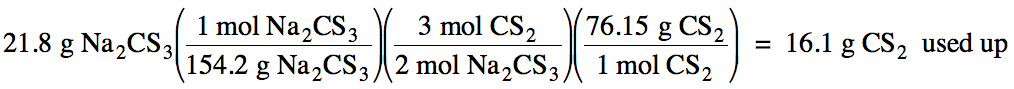
Finally, subtract the mass of CS2
used up from the initial mass of CS2 to calculate the excess mass of
CS2 remaining after the reaction is complete:
31.6 g
– 16.1 g = 15.5 g CS2 excess
Section 4-4: Percent Yield
The amount of a product calculated
using stoichiometry is known as the theoretical yield and represents the
maximum amount of the product that can form. However, for a variety of reasons, an amount less than the
theoretical yield of the product may actually be collected in the lab. This amount is known as the actual yield. The percent yield
of a reaction gives an indication of how close the actual yield is to the
theoretical yield:
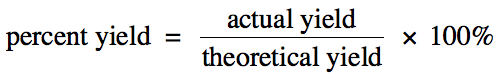
Note that any unit can be used to
calculate the percent yield.
Sample Exercise 4D:
Given the unbalanced equation
below, if 18 grams of solid copper reacts with an excess of aqueous AgNO3
and then 48 grams of solid silver is actually collected, what is the percent
yield of the reaction?
Cu (s) + AgNO3 (aq)
→ Cu(NO3)2
(aq) + Ag (s)
Solution:
First, balance the equation:
Cu (s) + 2 AgNO3 (aq)
→ Cu(NO3)2
(aq) + 2 Ag (s)
Next, use the mass of copper and stoichiometry to calculate the theoretical yield of silver
in grams since the actual yield of silver given in the problem is in grams, then divide the actual yield by the theoretical yield to
obtain the percent yield:
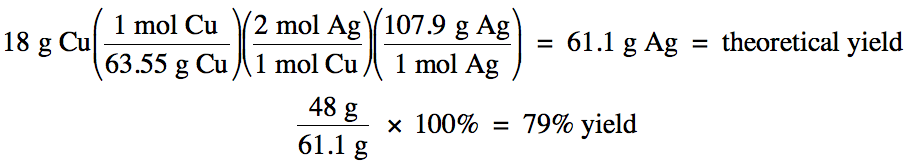
Chapter 4 Practice Exercises and Review Quizzes:
4-1) Balance
the following chemical equations using the smallest possible whole-number
coefficients:
(a) N2 + H2 → NH3
(b) C5H11OH +
O2 → CO2
+ H2O
Click for Solution
4-1) (a)
N2
+ H2 → 2 NH3
Final
Balanced Equation: N2 + 3 H2 → 2 NH3
(b)
C5H11OH
+ O2 → 5 CO2
+ H2O
C5H11OH
+ O2 → 5 CO2
+ 6 H2O
C5H11OH
+ 15/2 O2 → 5 CO2
+ 6 H2O
Final
Balanced Equation: 2 C5H11OH
+ 15 O2 → 10 CO2
+ 12 H2O
4-2)The density of solid KClO3 is 2.34 g/cm3. Given
the unbalanced equation below, if 415 cm3 of solid KClO3 react, how many kilograms of oxygen gas will be produced?
KClO3 (s) → KCl (s) + O2 (g)
Click for Solution
4-2)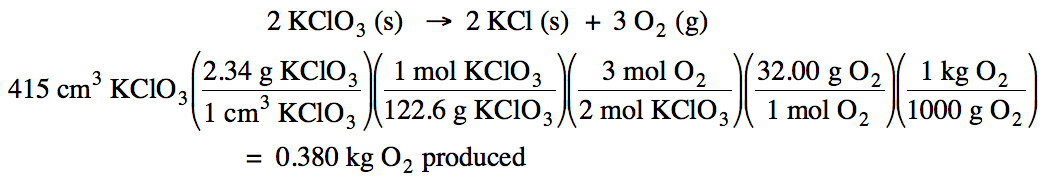
4-3) Given
the unbalanced equation below, if 2.24 grams of HF is mixed with 9.93 grams of
CCl4:
(a) Which is the limiting reagent?
(b) What maximum mass of CCl2F2
can form?
(c) What mass of the excess reagent
remains when the reaction is complete?
HF + CCl4 → HCl + CCl2F2
Click for Solution
4-3)
2 HF + CCl4 → 2 HCl + CCl2F2
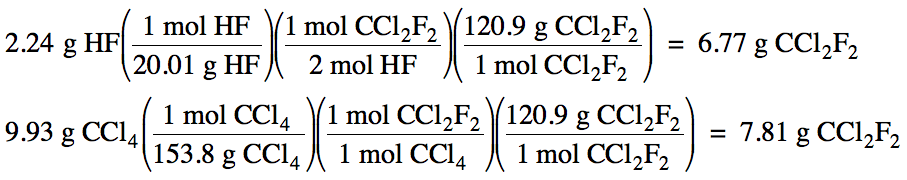
(a) HF produces less CCl2F2,
so HF is the limiting reagent.
(b) 6.77 g CCl2F2 maximum can form.
(c)
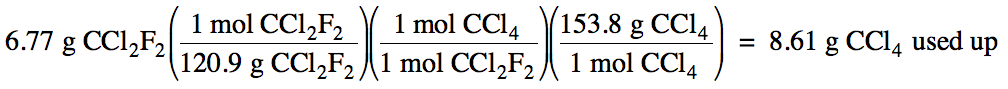
9.93 g - 8.61 g = 1.32 g CCl4 excess
4-4) Given the unbalanced equation
below, if 0.400 grams of solid CaH2 reacts with an excess of water
and then 0.0163 grams of hydrogen gas is actually collected, what is the
percent yield of the reaction?
CaH2 (s) + H2O
(l) → Ca(OH)2 (s) + H2
(g)
Click for Solution
4-4)
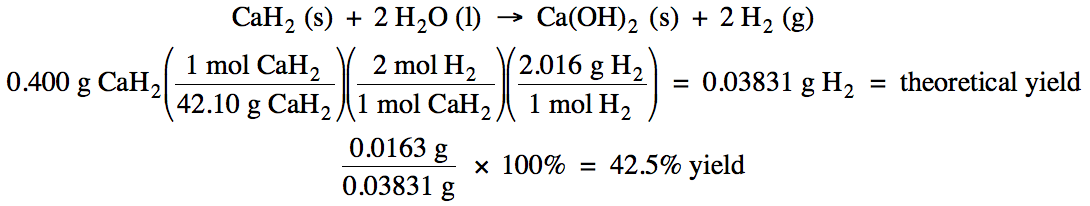
4-5) An 18 gram sample of a solid
mixture contains NaHCO3 as well as unreactive material. When heated, only the NaHCO3 in the mixture decomposes to produce 2.0 grams of CO2 according to
the following unbalanced equation:
NaHCO3 → Na2CO3 + H2O + CO2
What is the percent by mass of NaHCO3 in the
mixture?
Click for Solution
4-5)